大阪学習センター 客員教授 小林 治

新型コロナウィルス感染症の状況が厳しいなか勉強会も4月の初回後は休止が続いています。勉強会では円に関係する幾何学を現代の幾何学にまで及んで概観する予定でした。長い中断のため、参加された皆さんの中にはどのような展開になるのかイメージが得られない方もいらっしゃると思います。
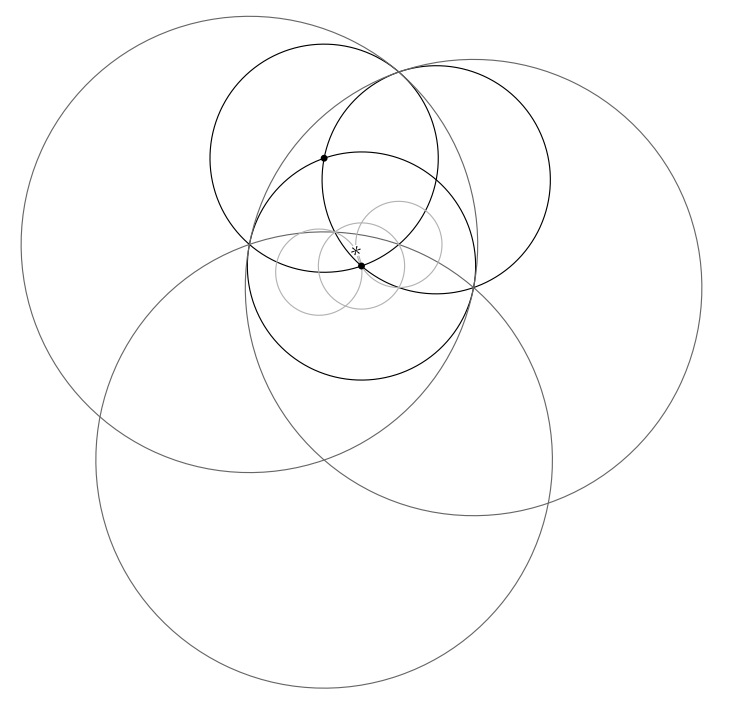
3層に重なった円の3密配置(triad of circles in a close position) からなるこの図はコンパスを用いて線分を7等分する方法を示しています。図の黒点を結ぶ(描かれてない) 線分を、この2点からコンパスのみを用いて到達できる星印の点が7 等分します。作図の正しさは中学校数学で証明できますが、その方法は術語を説明無しに用いると「7、13、11億1123万4567のように3で割ると1余る素数はZ[ω] でさらに素因数分解される」という整数論の事実に関係します。同じ発想で、フェルマーの最後の定理の3 次の場合「 x3 + y3 = z3を満たす正の整数はない」を、その証明を初等幾何学に翻訳することにより、高度な代数学を使わずに説明することができます。論証・計算に比べて感覚は不確かさが伴いますが、思考の飛躍を促し、その際しばしば図解が数式に勝る力を発揮します。円と並んで基本的な図形である直線の考察も、簡素でありながら深い理論を導きます。面接授業では直線の幾何学を取り上げる予定です。
勉強会の再開、面接授業の開講を楽しみにしています。
(2021年8月24日 小林 治)
大阪学習センター 機関誌「みおつくし」第83号より
公開日 2022-01-18 最終更新日 2022-12-18










